Upošteva se projekcija vektorja na os. Projekcije vektorjev na koordinatne osi. Projiciranje vektorja na os, ko je podan kot med vektorjem in osjo
Os je smer. Zato se projekcija na os ali na usmerjeno premico šteje za enako. Projekcija je lahko algebraična ali geometrijska. V geometrijskem smislu se projekcija vektorja na os razume kot vektor, v algebraičnem smislu pa je to število. To pomeni, da se uporabljata koncepta projekcije vektorja na os in numerične projekcije vektorja na os.
Če imamo os L in neničelni vektor A B → , potem lahko konstruiramo vektor A 1 B 1 ⇀ , ki označuje projekcije njegovih točk A 1 in B 1 .
A 1 B → 1 bo projekcija vektorja A B → na L .
Opredelitev 1
Projekcija vektorja na os imenujemo vektor, katerega začetek in konec sta projekciji začetka in konca danega vektorja. n p L A B → → običajno je označevati projekcijo A B → na L . Če želite zgraditi projekcijo na L, spustite navpičnice na L.
Primer 1
Primer projekcije vektorja na os.
Na koordinatni ravnini O x y je določena točka M 1 (x 1, y 1). Za podobo vektorja polmera točke M 1 je treba zgraditi projekcije na O x in O y. Dobimo koordinate vektorjev (x 1 , 0) in (0 , y 1) .

Če govorimo o projekciji a → na nenič b → ali projekciji a → na smer b → , potem mislimo na projekcijo a → na os, s katero sovpada smer b →. Projekcija a → na premico, ki jo definira b →, je označena z n p b → a → → . Znano je, da kadar je kot med a → in b → , lahko štejemo, da sta n p b → a → → in b → sosmerna. V primeru, ko je kot tup, sta n p b → a → → in b → nasprotno usmerjena. V primeru pravokotnosti a → in b → in a → je nič, je projekcija a → vzdolž smeri b → nič vektor.
Številčna značilnost projekcije vektorja na os je numerična projekcija vektorja na dano os.
2. opredelitev
Numerična projekcija vektorja na os pokličemo število, ki je enako zmnožku dolžine danega vektorja in kosinusa kota med danim vektorjem in vektorjem, ki določa smer osi.
Številčna projekcija A B → na L je označena z n p L A B → , a → na b → - n p b → a → .
Na podlagi formule dobimo npb → a → = a → · cos a → , b → ^ , od koder je a → dolžina vektorja a → , a ⇀ , b → ^ kot med vektorjema a → in b → .
Dobimo formulo za izračun številčne projekcije: n p b → a → = a → · cos a → , b → ^ . Uporablja se za znane dolžine a → in b → ter kot med njima. Formula je uporabna za znane koordinate a → in b → , vendar obstaja njena poenostavljena različica.
Primer 2
Ugotovite številčno projekcijo a → na premico v smeri b → z dolžino a → enako 8 in kotom med njima je 60 stopinj. Po pogoju imamo a ⇀ = 8 , a ⇀ , b → ^ = 60 ° . Torej, številčne vrednosti nadomestimo s formulo n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .
odgovor: 4.
Z znanimi cos (a → , b → ^) = a ⇀ , b → a → · b → , imamo a → , b → kot skalarni produkt a → in b → . Po formuli n p b → a → = a → · cos a ⇀, b → ^ lahko najdemo numerično projekcijo a → usmerjeno vzdolž vektorja b → in dobimo n p b → a → = a → , b → b → . Formula je enakovredna definiciji, navedeni na začetku klavzule.
Opredelitev 3
Številčna projekcija vektorja a → na os, ki sovpada v smeri z b →, je razmerje skalarnega produkta vektorjev a → in b → do dolžine b → . Formula n p b → a → = a → , b → b → je uporabna za iskanje numerične projekcije a → na premico, ki v smeri sovpada z b → , z znanimi koordinatama a → in b →.
Primer 3
Dano je b → = (- 3 , 4) . Poiščite numerično projekcijo a → = (1 , 7) na L .
Rešitev
Na koordinatni ravnini npb → a → = a → , b → b → ima obliko npb → a → = a → , b → b → = ax bx + ay bybx 2 + by 2 , za a → = (ax , ay ) in b → = bx , z . Za iskanje numerične projekcije vektorja a → na os L potrebujete: np L a → = npb → a → = a → , b → b → = ax bx + ay bybx 2 + by 2 = 1 (- 3 ) + 7 4 (- 3) 2 + 4 2 = 5 .
odgovor: 5.
Primer 4
Poiščite projekcijo a → na L , ki sovpada s smerjo b → , kjer sta a → = - 2 , 3 , 1 in b → = (3 , - 2 , 6) . Podan je tridimenzionalni prostor.
Rešitev
Glede na a → = a x , a y , a z in b → = b x , b y , b z izračunaj skalarni produkt: a ⇀ , b → = a x b x + a y b y + a z b z . Dolžino b → najdemo po formuli b → = b x 2 + b y 2 + b z 2. Iz tega sledi, da bo formula za določanje številčne projekcije a →: n p b → a ⇀ = a → , b → b → = a x b x + a y b y + a z b z b x 2 + b y 2 + b z 2 .
Nadomestne številčne vrednosti: np L a → = npb → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .
Odgovor: - 6 7 .
Poglejmo povezavo med a → na L in dolžino projekcije a → na L . Os L narišemo tako, da od točke do L dodamo a → in b →, nato pa narišemo pravokotno črto s konca a → na L in projiciramo na L. Obstaja 5 različic slike:

Prvič primer, ko a → = npb → a → → pomeni a → = npb → a → → , torej npb → a → = a → cos (a , → b → ^) = a → cos 0 ° = a → = npb → a → → .
Drugič primer pomeni uporabo n p b → a → ⇀ = a → cos a → , b → , torej n p b → a → = a → cos (a → , b →) ^ = n p b → a → → .
Tretji primer pojasnjuje, da kot npb → a → → = 0 → dobimo npb ⇀ a → = a → cos (a → , b → ^) = a → cos 90 ° = 0, nato npb → a → → = 0 in npb → a → = 0 = npb → a → → .
četrti primer kaže npb → a → → = a → cos (180 ° - a → , b → ^) = - a → cos (a → , b → ^) , sledi npb → a → = a → cos (a → , b → ^) = - npb → a → → .
peti primer kaže a → = npb → a → → , kar pomeni a → = npb → a → → , torej imamo npb → a → = a → cos a → , b → ^= a → cos 180 ° = - a → = - npb → a → .
Opredelitev 4
Številčna projekcija vektorja a → na os L , ki je usmerjena kot b → , ima pomen:
- dolžina projekcije vektorja a → na L pod pogojem, da je kot med a → in b → manjši od 90 stopinj ali enak 0: npb → a → = npb → a → → s pogojem 0 ≤ (a → , b →) ^< 90 ° ;
- nič pod pogojem pravokotnosti a → in b → : n p b → a → = 0, ko je (a → , b → ^) = 90 ° ;
- dolžina projekcije a → na L, krat -1, ko obstaja topel ali sploščen kot vektorjev a → in b → : n p b → a → = - n p b → a → → s pogojem 90°< a → , b → ^ ≤ 180 ° .
Primer 5
Glede na dolžino projekcije a → na L , enako 2 . Poiščite številčno projekcijo a → glede na to, da je kot 5 π 6 radianov.
Rešitev
Iz pogoja je razvidno, da je ta kot tup: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .
Odgovor: - 2.
Primer 6
Dana je ravnina O x y z z dolžino vektorja a → enako 6 3 , b → (- 2 , 1 , 2) s kotom 30 stopinj. Poiščite koordinate projekcije a → na os L.
Rešitev
Najprej izračunamo numerično projekcijo vektorja a → : n p L a → = n p b → a → = a → cos (a → , b →) ^ = 6 3 cos 30 ° = 6 3 3 2 = 9 .
Po pogoju je kot oster, potem je numerična projekcija a → = dolžina projekcije vektorja a → : n p L a → = n p L a → → = 9 . Ta primer kaže, da sta vektorja n p L a → → in b → sousmerjena, kar pomeni, da obstaja število t, za katerega velja enakost: n p L a → → = t · b → . Od tu vidimo, da je np L a → → = tb → , zato lahko najdemo vrednost parametra t: t = np L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .
Potem so np L a → → = 3 b → s koordinatami projekcije vektorja a → na os L b → = (- 2 , 1 , 2) , kjer je treba vrednosti pomnožiti s 3 Imamo np L a → → = (- 6 , 3 , 6). Odgovor: (- 6 , 3 , 6) .
Ponoviti je treba predhodno preučene podatke o stanju kolinearnosti vektorja.
Če opazite napako v besedilu, jo označite in pritisnite Ctrl+Enter
Pustimo dva vektorja in sta dana v prostoru. Odložite od poljubne točke O vektorji in. kotiček med vektorjema in se imenuje najmanjši kot. Označeno ![]() .
.

Upoštevajte os l in nanj narišite vektor enote (to je vektor, katerega dolžina je enaka eni).

Kot med vektorjem in osjo l razumeti kot med vektorjema in .
Torej naj l je neka os in je vektor.
Označi z A 1 in B1 projekcije na os l točke A in B. Pretvarjajmo se A 1 ima koordinato x 1, ampak B1- koordinata x2 na osi l.

Potem projekcija vektor na os l se imenuje razlika x 1 – x2 med koordinatami projekcij konca in začetka vektorja na to os.
Projekcija vektorja na os l bomo označili.
Jasno je, da če je kot med vektorjem in osjo l ostra potem x2> x 1, in projekcijo x2 – x 1> 0; če je ta kot tup, potem x2< x 1 in projekcija x2 – x 1< 0. Наконец, если вектор перпендикулярен оси l, potem x2= x 1 in x2– x 1=0.

Tako je projekcija vektorja na os l je dolžina segmenta A 1 B 1 vzeto z določenim znakom. Zato je projekcija vektorja na os število ali skalar.
Podobno definiramo projekcijo enega vektorja na drugega. V tem primeru najdemo projekcije koncev tega vektorja na premici, na kateri leži 2. vektor.
Oglejmo si nekaj glavnih projekcijske lastnosti.
LINEARNO ODVISNI IN LINEARNO NEODVISNI SISTEMI VEKTORJEV
Razmislimo o več vektorjih.
Linearna kombinacija od teh vektorjev je kateri koli vektor oblike , kjer so nekaj številk. Številke imenujemo koeficienti linearne kombinacije. Rečeno je tudi, da je v tem primeru linearno izraženo v smislu danih vektorjev, t.j. pridobljeni iz njih z linearnimi operacijami.
Na primer, če so podani trije vektorji, se vektorji lahko obravnavajo kot njihova linearna kombinacija: ![]()
Če je vektor predstavljen kot linearna kombinacija nekaterih vektorjev, potem rečemo, da je razpadla vzdolž teh vektorjev.
Vektorji se imenujejo linearno odvisna, če obstajajo takšne številke, niso vsa enaka nič, to ![]() . Jasno je, da bodo dani vektorji linearno odvisni, če je kateri od teh vektorjev linearno izražen z drugimi.
. Jasno je, da bodo dani vektorji linearno odvisni, če je kateri od teh vektorjev linearno izražen z drugimi.
Sicer pa t.j. ko je razmerje ![]() izvaja samo takrat, ko
izvaja samo takrat, ko ![]() , se ti vektorji imenujejo linearno neodvisna.
, se ti vektorji imenujejo linearno neodvisna.
Izrek 1. Vsaka dva vektorja sta linearno odvisna, če in samo če sta kolinearna.
Dokaz:
Podobno je mogoče dokazati naslednji izrek.
2. izrek. Trije vektorji so linearno odvisni, če in samo če so koplanarni.
Dokaz.
OSNOVA
Osnova je zbirka neničel linearno neodvisnih vektorjev. Elemente osnove bomo označili z .
V prejšnjem pododdelku smo videli, da sta dva nekolinearna vektorja v ravnini linearno neodvisna. Zato sta po izreku 1 iz prejšnjega odstavka osnova na ravnini katera koli dva nekolinearna vektorja na tej ravnini.
Podobno so kateri koli trije nekoplanarni vektorji linearno neodvisni v prostoru. Zato se trije nekoplanarni vektorji imenujejo baza v prostoru.
Naslednja trditev drži.
Izrek. Naj bo osnova podana v prostoru. Potem lahko kateri koli vektor predstavimo kot linearno kombinacijo ![]() , kje x, y, z- nekaj številk. Takšna razgradnja je edinstvena.
, kje x, y, z- nekaj številk. Takšna razgradnja je edinstvena.
Dokaz.
Tako vam osnova omogoča edinstveno pridruževanje vsakega vektorja s trojko številk - koeficienti razširitve tega vektorja glede na vektorje osnove: . Velja tudi obratno, vsaka trojka številk x, y, z z uporabo osnove lahko vektor povežete, če naredite linearno kombinacijo ![]() .
.
Če je osnova in ![]() , nato številke x, y, z poklical koordinate vektorji v dani osnovi. Vektorske koordinate označujejo .
, nato številke x, y, z poklical koordinate vektorji v dani osnovi. Vektorske koordinate označujejo .
KARTEZIJSKI KOORDINATNI SISTEM
Naj bo podana točka v prostoru O in tri nekomplanarne vektorje.

Kartezijev koordinatni sistem v prostoru (na ravnini) se imenuje množica točke in osnove, t.j. množica točke in treh nekoplanarnih vektorjev (2 nekolinearna vektorja), ki izhajajo iz te točke.
Dot O imenovano izvor; ravne črte, ki potekajo skozi izvor v smeri osnovnih vektorjev, se imenujejo koordinatne osi - abscisa, ordinatna in aplicirana os. Ravnine, ki potekajo skozi koordinatne osi, se imenujejo koordinatne ravnine.

Razmislite o poljubni točki v izbranem koordinatnem sistemu M. Uvedemo pojem koordinata točke M. Vektor, ki povezuje izvor s točko M. poklical radij vektor točke M.

Vektor v izbrani osnovi lahko povežemo s trojko številk - njegove koordinate: ![]() .
.
Koordinate vektorja polmera točke M. poklical koordinate točke M. v obravnavanem koordinatnem sistemu. M(x,y,z). Prva koordinata se imenuje abscisa, druga je ordinata, tretja pa aplikat.

Kartezijeve koordinate na ravnini so definirane podobno. Tukaj ima točka samo dve koordinati - absciso in ordinato.
Preprosto je videti, da ima za dani koordinatni sistem vsaka točka določene koordinate. Po drugi strani pa za vsako trojko števil obstaja ena sama točka, ki ima ta števila kot koordinate.
Če imajo vektorji, vzeti za osnovo v izbranem koordinatnem sistemu, enotno dolžino in so parno pravokotni, se koordinatni sistem imenuje Kartezijanski pravokotnik.

To je enostavno pokazati.
Smerni kosinusi vektorja v celoti določajo njegovo smer, o njegovi dolžini pa ničesar.
Opredelitev 1. Na ravnini je vzporedna projekcija točke A na os l točka - presečna točka osi l z ravno črto, vlečeno skozi točko A vzporedno z vektorjem, ki določa smer projekcije.
Definicija 2. Vzporedna projekcija vektorja na l-os (na vektor) je koordinata vektorja glede na osnovo os l, kjer sta točki in vzporedni projekciji točk A oziroma B na os l (slika 1).
Po definiciji imamo
Opredelitev 3. če in osnovo osi l kartezijska, torej projekcija vektorja na os l imenujemo ortogonalno (slika 2).
V prostoru ostaja v veljavi definicija 2 projekcije vektorja na os, le smer projekcije podata dva nekolinearna vektorja (slika 3).

Iz definicije projekcije vektorja na os sledi, da je vsaka koordinata vektorja projekcija tega vektorja na os, ki jo določa ustrezni bazni vektor. V tem primeru je smer načrtovanja določena z dvema osnovnima vektorjema, če se načrtovanje izvaja (upošteva) v prostoru, ali z drugim baznim vektorjem, če načrtovanje obravnavamo na ravnini (slika 4).

Izrek 1. Ortogonalna projekcija vektorja na l-os je enaka zmnožku modula vektorja in kosinusa kota med pozitivno smerjo l-osi in, t.j.

Po drugi strani
Od najdemo
Če nadomestimo AC z enakostjo (2), dobimo
Od številk x in enakega predznaka v obeh obravnavanih primerih ((slika 5, a) ; (slika 5, b) , potem enakost (4) pomeni
Komentar. V prihodnosti bomo upoštevali le pravokotno projekcijo vektorja na os, zato bo beseda "orth" (ortogonalno) v zapisu izpuščena.
Predstavljamo številne formule, ki jih bomo uporabljali v prihodnosti pri reševanju problemov.
a) Projekcija vektorja na os.
Če, potem ima ortogonalna projekcija na vektor po formuli (5) obliko
c) Razdalja od točke do ravnine.

Naj bo b podana ravnina z normalnim vektorjem, M dana točka,
d - razdalja od točke M do ravnine b (slika 6).
Če je N poljubna točka ravnine b in sta projekciji točk M in N na os, potem
- G) Razdalja med sekajočimi se črtami.

Naj bosta a in b dani sekajoči se premici, vektor, pravokotni nanje, A in B sta poljubni točki premic a in b (slika 7) in projekciji točk A in B na, potem
e) Razdalja od točke do premice.
Naj bo l- dana premica z vektorjem smeri, M - podana točka,
N - njegova projekcija na črto l, nato - želena razdalja (slika 8).
Če je A poljubna točka na premici l, potem v pravokotnem trikotniku MNA najdemo hipotenuzo MA in krake. pomeni,

e) Kot med premico in ravnino.

Naj je smerni vektor dane črte l, - vektor normale dane ravnine b, - projekcija premice l na ravnino b (slika 9).
Kot veste, je kot q med črto l in njeno projekcijo na ravnino b imenujemo kot med premico in ravnino. Imamo
Naj navedemo primere reševanja metričnih problemov z vektorsko-koordinatno metodo.
Na voljo bodo tudi naloge za samostojno rešitev, na katere si lahko ogledate odgovore.
Vektorski koncept
Preden se naučite vse o vektorjih in operacijah z njimi, se prilagodite reševanju preproste težave. Obstaja vektor vašega podjetja in vektor vaših inovativnih sposobnosti. Vektor podjetnosti te pripelje do cilja 1, vektor inovativnih sposobnosti pa do cilja 2. Pravila igre so takšna, da se ne moreš premikati v smereh teh dveh vektorjev hkrati in doseči dva cilja hkrati. Vektorji medsebojno delujejo ali, matematično gledano, se na vektorjih izvede neka operacija. Rezultat te operacije je vektor »Rezultat«, ki vas pripelje do cilja 3.
Zdaj mi povejte: rezultat katere operacije na vektorjih "Podjetje" in "Inovativne sposobnosti" je vektor "Rezultat"? Če ne morete povedati takoj, ne bodite malodušni. Ko boste študirali to lekcijo, boste lahko odgovorili na to vprašanje.
Kot smo videli zgoraj, vektor nujno prihaja iz neke točke A v ravni črti do neke točke B. Posledično ima vsak vektor ne le številčno vrednost - dolžino, temveč tudi fizično in geometrijsko - smer. Iz tega izhaja prva, najenostavnejša definicija vektorja. Torej, vektor je usmerjen segment, ki poteka od točke A do točke B. Označeno je takole:

In začeti drugače vektorske operacije , se moramo seznaniti še z eno definicijo vektorja.
Vektor je neke vrste predstavitev točke, ki jo je treba doseči z neke izhodiščne točke. Na primer, tridimenzionalni vektor je običajno zapisan kot (x, y, z) . Preprosto povedano, te številke predstavljajo, kako daleč morate iti v treh različnih smereh, da pridete do točke.
Naj je podan vektor. Pri čemer x = 3 (desna roka kaže na desno) y = 1 (leva roka kaže naprej) z = 5 (pod točko je lestev, ki vodi navzgor). Iz teh podatkov boste točko našli tako, da se sprehodite 3 metre v smeri, ki jo označuje desno roko, nato 1 meter v smeri, ki jo kaže leva roka, nato pa vas čaka lestev in, ko se povzpnete 5 metrov, se končno znajdete na končni točki.
Vsi ostali izrazi so izpopolnitve zgoraj predstavljene razlage, potrebne za različne operacije z vektorji, torej za reševanje praktičnih problemov. Pojdimo skozi te strožje definicije in se osredotočimo na tipične vektorske probleme.
Fizični primeri vektorske količine so lahko premik materialne točke, ki se giblje v prostoru, hitrost in pospešek te točke, pa tudi sila, ki deluje nanjo.

geometrijski vektor predstavljena v dvodimenzionalnem in tridimenzionalnem prostoru v obliki usmerjen segment. To je segment, ki ima začetek in konec.
Če A je začetek vektorja in B- njegov konec, potem je vektor označen s simbolom ali ena male črke. Na sliki je konec vektorja označen s puščico (slika 1)
Dolžina(oz modul) geometrijskega vektorja je dolžina segmenta, ki ga generira
Oba vektorja se imenujeta enako , če jih je mogoče združiti (ko smeri sovpadajo) z vzporednim prevajanjem, t.j. če sta vzporedna, kažeta v isto smer in imata enake dolžine.
V fiziki se pogosto upošteva pripeti vektorji, podano z aplikacijsko točko, dolžino in smerjo. Če točka uporabe vektorja ni pomembna, ga lahko prenesemo, pri čemer ohranimo dolžino in smer na katero koli točko v prostoru. V tem primeru se vektor imenuje prost. Strinjamo se, da bomo upoštevali le prosti vektorji.
Linearne operacije na geometrijskih vektorjih

Pomnožite vektor s številom
Vektorski izdelek na številko Vektor se imenuje vektor, ki je pridobljen iz vektorja z raztezanjem (na ) ali krčenjem (v ) krat, smer vektorja pa se ohrani, če , in obrnjena, če . (slika 2)
Iz definicije sledi, da se vektorja in = vedno nahajata na eni ali vzporednih premicah. Takšni vektorji se imenujejo kolinearno. (Lahko rečete tudi, da so ti vektorji vzporedni, vendar je v vektorski algebri običajno reči "kolinearno".) Velja tudi obratno: če sta vektorja in kolinearna, sta povezana z relacijo
Zato enakost (1) izraža pogoj kolinearnosti dveh vektorjev.

Vektorsko seštevanje in odštevanje
Pri dodajanju vektorjev morate to vedeti vsota vektorji in se imenuje vektor, katerega začetek sovpada z začetkom vektorja, konec pa s koncem vektorja, pod pogojem, da je začetek vektorja pritrjen na konec vektorja. (slika 3)

To definicijo lahko razdelimo na poljubno končno število vektorjev. Naj v prostoru dano n prosti vektorji. Pri dodajanju več vektorjev se njihova vsota vzame kot zaključni vektor, katerega začetek sovpada z začetkom prvega vektorja, konec pa s koncem zadnjega vektorja. Se pravi, če je začetek vektorja pritrjen na konec vektorja, začetek vektorja pa na konec vektorja itd. in končno do konca vektorja - začetka vektorja, potem je vsota teh vektorjev končni vektor ![]() , katerega začetek sovpada z začetkom prvega vektorja in katerega konec sovpada s koncem zadnjega vektorja . (slika 4)
, katerega začetek sovpada z začetkom prvega vektorja in katerega konec sovpada s koncem zadnjega vektorja . (slika 4)
Izrazi se imenujejo komponente vektorja, formulirano pravilo pa je pravilo poligona. Ta mnogokotnik morda ni raven.
Ko vektor pomnožimo s številom -1, dobimo nasprotni vektor. Vektorji in imajo enako dolžino in nasprotni smeri. Njihova vsota daje ničelni vektor, katerega dolžina je nič. Smer ničelnega vektorja ni definirana.
V vektorski algebri operacije odštevanja ni treba obravnavati ločeno: odšteti vektor od vektorja pomeni vektorju dodati nasprotni vektor, t.j. ![]()
Primer 1 Poenostavite izraz:
![]() .
.
 ,
,
to pomeni, da lahko vektorje seštevamo in množimo s številkami na enak način kot polinome (zlasti tudi težave za poenostavitev izrazov). Običajno se pred izračunom produktov vektorjev pojavi potreba po poenostavitvi linearno podobnih izrazov z vektorji.
Primer 2 Vektorji in služijo kot diagonale paralelograma ABCD (slika 4a). Izrazite v smislu in vektorji , , in , ki so strani tega paralelograma.

Rešitev. Presečišče diagonal paralelograma prepolovi vsako diagonalo. Dolžine vektorjev, zahtevane v pogoju problema, najdemo bodisi kot polovico vsote vektorjev, ki tvorijo trikotnik z želenimi, ali kot polovico razlik (odvisno od smeri vektorja, ki služi kot diagonala), ali, kot v zadnjem primeru, polovico vsote, vzete s predznakom minus. Rezultat so vektorji, potrebni za pogoj problema:

Obstajajo vsi razlogi za domnevo, da ste zdaj pravilno odgovorili na vprašanje o vektorjih "Podjetje" in "Inovativne sposobnosti" na začetku te lekcije. Pravilen odgovor: ti vektorji so podvrženi operaciji seštevanja.
Sami rešite probleme na vektorjih, nato pa si oglejte rešitve
Kako najti dolžino vsote vektorjev?
Ta problem zavzema posebno mesto pri operacijah z vektorji, saj vključuje uporabo trigonometričnih lastnosti. Recimo, da imate nalogo, kot je naslednja:
Glede na dolžino vektorjev ![]() in dolžino vsote teh vektorjev. Poiščite dolžino razlike teh vektorjev.
in dolžino vsote teh vektorjev. Poiščite dolžino razlike teh vektorjev.
Rešitve tega in drugih podobnih problemov ter pojasnila, kako jih rešiti - v lekciji " Seštevanje vektorjev: dolžina vsote vektorjev in kosinusni izrek ".
Rešitev takšnih težav lahko preverite na Spletni kalkulator "Neznana stranica trikotnika (vektorski seštevek in kosinusni izrek)" .
Kje so produkti vektorjev?
Produkti vektorja z vektorjem niso linearne operacije in se obravnavajo ločeno. In imamo lekcije "Točkovni produkt vektorjev" in "Vektorski in mešani produkt vektorjev".
Projekcija vektorja na os
Projekcija vektorja na os je enaka zmnožku dolžine projekcijskega vektorja in kosinusa kota med vektorjem in osjo:
![]()
Kot je znano, projekcija točke A na premici (ravnini) je osnova navpičnice, spuščena s te točke na premico (ravnino).

Naj - poljuben vektor (slika 5) in in - projekcije njegovega začetka (točke A) in konec (pike B) na os l. (Za sestavljanje projekcije točke A) potegnite naravnost skozi točko A ravnina, pravokotna na premico. Presečišče premice in ravnine bo določilo zahtevano projekcijo.
Komponenta vektorja na osi l imenujemo tak vektor, ki leži na tej osi, katerega začetek sovpada s projekcijo začetka, konec pa s projekcijo konca vektorja.
Projekcija vektorja na os l poklicali številko
![]() ,
,
enaka dolžini sestavnega vektorja na tej osi, vzeta z znakom plus, če smer komponente sovpada s smerjo osi l, in z znakom minus, če sta si smeri nasprotni.
Glavne lastnosti vektorskih projekcij na os:
1. Projekcije enakih vektorjev na isto os so med seboj enake.
2. Ko se vektor pomnoži s številom, se njegova projekcija pomnoži z istim številom.
3. Projekcija vsote vektorjev na katero koli os je enaka vsoti projekcij na isto os členov vektorjev.
4. Projekcija vektorja na os je enaka zmnožku dolžine projekcijskega vektorja in kosinusa kota med vektorjem in osjo:
![]()
 .
.

Rešitev. Projicirajmo vektorje na os l kot je opredeljeno v zgornji teoretični referenci. Iz slike 5a je razvidno, da je projekcija vsote vektorjev enaka vsoti projekcij vektorjev. Izračunamo te projekcije:

Najdemo končno projekcijo vsote vektorjev:
Razmerje vektorja s pravokotnim kartezijskim koordinatnim sistemom v prostoru
Spoznavanje z pravokotni kartezijev koordinatni sistem v prostoru je potekal v ustrezni lekciji, po možnosti odprite v novem oknu.
V urejenem sistemu koordinatnih osi 0xyz osi Ox poklical os x, os 0y – y-os, in os 0z – aplicirana os.

s poljubno točko M vektor vesoljske vezi
poklical radij vektor točke M in ga projicira na vsako od koordinatnih osi. Označimo vrednosti ustreznih projekcij:
Številke x, y, z poklical koordinate točke M, oz abscisa, ordinate in aplikacija, in so zapisani kot urejena točka števil: M(x; y; z)(slika 6).
Imenuje se vektor enotne dolžine, katerega smer sovpada s smerjo osi vektor enote(oz ortom) osi. Označi z
V skladu s tem so enotni vektorji koordinatnih osi Ox, oj, Oz
![]()
Izrek. Vsak vektor je mogoče razstaviti na enotne vektorje koordinatnih osi:

![]() (2)
(2)
Enakost (2) imenujemo razširitev vektorja vzdolž koordinatnih osi. Koeficienti te ekspanzije so projekcije vektorja na koordinatne osi. Tako so ekspanzijski koeficienti (2) vektorja vzdolž koordinatnih osi koordinate vektorja.
Po izbiri določenega koordinatnega sistema v prostoru se vektor in trojka njegovih koordinat enolično določita, tako da lahko vektor zapišemo v obliki
Vektorski predstavitvi v obliki (2) in (3) sta enaki.
Stanje kolinearnih vektorjev v koordinatah
Kot smo že omenili, vektorje imenujemo kolinearni, če so povezani z relacijo
Naj vektorji ![]() . Ti vektorji so kolinearni, če so koordinate vektorjev povezane z relacijo
. Ti vektorji so kolinearni, če so koordinate vektorjev povezane z relacijo
![]() ,
,
to pomeni, da so koordinate vektorjev sorazmerne.
Primer 6 Dani vektorji ![]() . Ali so ti vektorji kolinearni?
. Ali so ti vektorji kolinearni?
Rešitev. Ugotovimo razmerje med koordinatami teh vektorjev:
![]() .
.
Koordinate vektorjev so sorazmerne, zato so vektorji kolinearni ali, kar je enako, vzporedni.
Dolžina vektorja in kosinus smeri
Zaradi medsebojne pravokotnosti koordinatnih osi je dolžina vektorja
![]()
je enaka dolžini diagonale pravokotnega paralelepipeda, zgrajenega na vektorjih
in je izražena z enakostjo
![]() (4)
(4)
Vektor je v celoti definiran z določitvijo dveh točk (začetek in konec), tako da lahko koordinate vektorja izrazimo s koordinatami teh točk.
Naj bo začetek vektorja v danem koordinatnem sistemu v točki
in konec je na točki


Od enakosti
Sledi temu
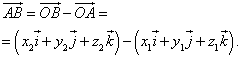
ali v koordinatni obliki
posledično koordinate vektorja so enake razlikam istoimenskih koordinat konca in začetka vektorja . Formula (4) ima v tem primeru obliko
Smer vektorja je določena smerni kosinusi . To so kosinusi kotov, ki jih vektor naredi z osmi Ox, oj in Oz. Označimo te kote oz α , β in γ . Potem lahko kosinuse teh kotov najdemo s formulami
Smerni kosinusi vektorja so tudi koordinate vektorja vektorja in s tem vektorja vektorja
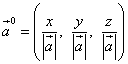
![]() .
.
Glede na to, da je dolžina vektorskega vektorja enaka eni enoti, tj.
![]() ,
,
dobimo naslednjo enakost za smerne kosinuse:
Primer 7 Poiščite dolžino vektorja x = (3; 0; 4).
Rešitev. Dolžina vektorja je
![]()
Primer 8 Podane točke:
Ugotovite, ali je trikotnik, zgrajen na teh točkah, enakokraki.
Rešitev. S formulo dolžine vektorja (6) poiščemo dolžine stranic in ugotovimo, ali sta dve enaki:

Najdeni sta bili dve enaki strani, tako da ni treba iskati dolžine tretje strani, dani trikotnik pa je enakokraki.
Primer 9 Poiščite dolžino vektorja in njegove smerne kosinuse, če ![]() .
.
Rešitev. Vektorske koordinate so podane:
![]() .
.
Dolžina vektorja je enaka kvadratnemu korenu vsote kvadratov vektorjevih koordinat:
![]() .
.
Iskanje smernih kosinusov:

Sami rešite problem z vektorji, nato pa poglejte rešitev
Operacije z vektorji, podanimi v koordinatni obliki
Naj sta podana dva vektorja in podana z njihovimi projekcijami:
![]()
![]()
Označimo dejanja na teh vektorjih.

 vhod
vhod